在线匹配问题是在线算法研究领域一个核心模型,本文将为大家介绍在线匹配问题的研究背景以及刊登在JACM 2020上关于全在线匹配(Fully Online Matching)的主要内容。此前关于在线匹配问题的研究主要局限于二分图中的单侧在线模式,仅能刻画在线到达用户与离线资源之间的匹配问题。论文提出了全在线匹配模型,允许问题中所有顶点均在线到达。同时,以全在线模式为切入点,论文将一般图引入了模型之中,对1990年开放至今的在线匹配问题一般图分析难题做出了首次突破。
什么是在线匹配问题?
传统组合优化问题的主要特点和挑战是在收到一个完整的输入之后,如何快速且精确地求出优化目标。而在线问题则放宽了“完整输入”这一要求,允许输入随时间逐渐给出。我们需要在特定的时间点上,根据已有的部分输入,做出即时的在线决策,并保障一定的长期的优化效果。现实生活中所有许多实际场景,其实都面临了上述不完全信息的挑战:例如,在在线广告投放中,网站需要在用户访问的短时间内,做出即时的投放决策。自然地,网站希望优化其投放策略的长期收益,但如何在不知道未来的情况下做出优秀的投放决策呢?这就是在线算法所关注的话题。
最大(二分图)匹配问题是最为经典和简洁的图论组合优化问题之一,其重要性不言而喻。匹配问题的在线模型也很自然地成为了在线优化中最早被探索的问题之一,并长期处于在线优化领域的核心地位。在STOC90会议中,Karp, Vazirani和Vazirani三位学者首次提出了在线二分图匹配模型:假设存在一个潜在的二分图 其中一侧顶点为离线顶点(直接给定),而另一侧顶点为在线顶点(逐步到达)。我们要求算法在任何一个在线顶点输入的时间点(此时与中顶点的边同时给出),即时地决定是否将与中某一相邻顶点匹配,并且决策不能反悔。模型的优化目标为最大化最终的匹配边数。我们可以用该模型重新审视广告投放的例子,假设一条广告仅能投放一次(一种广告可以被想象成很多条),我们可以把广告看作离线点,用户看作在线点,他们之间是否有边则代表了是否适合将某条广告投放给某个用户。由此,算法在线匹配的过程即可被看作投放的过程,在线二分图匹配模型成功刻画了广告投放的实际场景。
在在线优化研究中最为常用的方法称为竞争比分析方法,即以竞争比来衡量某个在线算法的性能。在线匹配问题中,竞争比的定义如下:如果一个在线算法在任何可能的图以及任何可能的在线顶点到达顺序中,均能保证其在线解大于图离线最大匹配的倍,那么我们就称该算法为-竞争的。在Karp等人的工作中,他们首先证明了贪心算法(在在线顶点到达时任意匹配一个仍未匹配的离线点)可以达到0.5竞争比,且0.5竞争比是所有确定性在线算法可以达到的最好竞争比。那么我们是否可以利用随机算法突破0.5竞争比?Karp等人同样针对该问题做出了回答,提出了著名的RANKING算法(将离线点提前随机排序,在线点则直接根据该顺序来进行匹配决策)。他们证明了该算法可以达到竞争比,且该竞争比是任何随机算法能达到的最优竞争比。
有人可能会问,既然Karp等人的工作已经同时找到了确定性算法和随机算法所能达到的最优竞争比,那么故事是不是就到此结束了?我们回顾在线二分图匹配模型,发现其具有一些局限性。该模型只关注了匹配边的数量,而忽视了匹配边之间可能存在的收益差别。其次,该模型只考虑单侧顶点在线到达的模式,局限了模型的适用范围。此外,该模型仅针对了二分图的特殊情况,而没有考虑一般图。实际上,早在1990年的论文之中,Karp等人已经提出了“RANKING算法是否在非二分图中也是最优算法”的开放问题。然而,在近30年的研究之中,研究者没有成功找到一般图中突破0.5竞争比的分析方法。
如何建模顶点全在线的在线匹配问题?
在JACM20中,我们重点关注了如何应对顶点全在线到达的挑战,以及如何将模型拓展到一般图上。让我们先从顶点全在线说起,在如今许多P2P应用场景中,匹配的双方从用户和资源转换成了用户和用户。例如,在滴滴打车应用中,司机和乘客同时作为在线顶点出现,我们并不能假设其中的一侧作为离线点提前给定。应对这一挑战,我们提出了可以刻画该类场景的全在线匹配模型:假设存在一个潜在的二分图,所有的顶点均为在线顶点,他们拥有两个关键时间节点,到达时间以及离开时间。在某个顶点的到达时间,该顶点和系统中已到达顶点(未离开)之间的边被输入。我们需要在顶点的离开时刻前,决定是否将其与某个与其相邻的顶点匹配,目标仍是最大化匹配边数。与上述应用场景结合起来说,到达时刻就是用户发起请求的时间,而离开时间就是用户不愿意再等待匹配的时间点。在该模型中,我们依然可以证明贪心算法已经足够达到确定型算法可以达到的最优竞争比0.5。那么,如果允许随机性,我们能达到多少竞争比,是否能够至少突破0.5呢?
此外,在原有单侧在线模型中,推广到一般图问题并不直接,因为原问题二分图的两侧具有离线和在线的不同性质。然而,在全在线模式下,一般图拓展变得非常自然,由于所有顶点均为在线,我们只需要将潜在图G的二分图限定取消即可。从应用角度,一般图具备更强的刻画性能,例如:考虑我们现在需要对乘客和乘客之间进行拼车的匹配,而不是乘客和司机,该场景就需要用到一般图来刻画。从理论角度,全在线匹配模型很好地成为了研究一般图在线匹配,并回答Karp等人1990年提出的开放问题的切人点。其中蕴含的理论难题包括:RANKING算法在一般图中是否仍然是最优算法、一般图中最好的随机算法能达到多少竞争比、一般图是否严格难于二分图等。
在JACM20中,我们分别针对上述理论问题,做出了相应的分析。首先,对限定于二分图的全在线匹配问题,我们证明了RANKING算法同样可以突破竞争比,并达到竞争。我们同时举出紧的例子,证明了RANKING算法在全在线模型中能达到的最好竞争比即为,劣于单侧在线模型的。其次,对于一般图,我们同样分析了RANKING算法的性能,证明RANKING算法为-竞争,成功突破。然而,我们尚未给出对应例子来证明RANKING算法无法突破,其竞争比上界仅和二分图中的相同。所以,在竞争比角度,RANKING算法在一般图与二分图的表现是否有严格区别,仍然属于开放问题。最后,从模型本身的难度出发,我们证明了任何随机算法都不能在全在线问题中(即使限定二分图)突破竞争比,小于1-1/e≈0.632。这说明了全在线匹配模型在竞争比角度严格难于单侧的在线二分图匹配模型。
在后续研究中,上述部分结果已经得到了改进。在FOCS20中,RANKING算法被改进为Balanced RANKING,并被证明可以达到0.569竞争比。在2022年最新的研究工作中[Preprint22],全在线匹配的一般上界降到了0.613。以下,我们将简单介绍JACM20论文中所采用的算法分析框架,以及使得分析成功的关键性质。
如何在全在线模型中分析RANKING算法?
首先,我们需要先在全在线模型中定义RANKING算法。易知提前做决策没有任何好处,我们规定算法仅在某个顶点的离开时间做出匹配决策。与单侧模型中RANKING算法一致,我们希望匹配决策由一个预先随机的rank决定,但现在有以下区别:
(1) 我们需要对所有顶点都采样rank,因为决策可能发生于任何一个顶点的离开时间。
(2) 由于顶点均为在线到达,我们无法提前对所有顶点进行排序。
为解决上述问题,我们采用如下解决方法:在顶点的到达时间,在[0,1]区间内均匀采样一个随机数,并以此作为顶点的rank,以此来达到和提前随机排序一样的随机效果。而在顶点的离开时刻,我们会根据其未匹配相邻顶点的rank大小,优先选择最小rank的顶点进行匹配。至此,我们的算法定义完成。
我们试图使用在线随机原始对偶分析方法来进行分析。我们首先需要解决的问题是:如何在全在线模式下定义收益分配策略。我们引入了主动匹配和被动匹配的概念:如果匹配发生于某个顶点u的离开时刻,我们定义u在进行主动匹配,而被u选择的v则是被被动匹配。以原单侧在线的在线二分图匹配模型为例,在线顶点永远在进行主动匹配,而离线顶点永远是被动匹配。在该定义下,我们可以很自然将单侧模型中的收益分配策略拓展过来。定义弱递增的收益分配函数g(y),若一条边(u,v)被匹配,将g(yv)的收益分配给其中的被动顶点v,而1-g(yv)分配给其中的主动顶点u。我们能不能通过这一拓展得到与单侧二分图匹配模型一样的不等式(A)呢?答案是否定的,因为使得不等式(A)成功的两个关键性质在全在线模型中并不成立。
首先考虑限定二分图的全在线匹配模型,虽然我们可以证明性质2仍然成立,但性质1并不一定成立。这是因为即使v不匹配,u可能处于被动匹配状态,并没有进行选择,所以不一定能获得1-g(θ)的收益。
为解决这一困难,我们考虑了更复杂的匹配状态变化过程。我们同时考虑u和v的rank变化而不只是其中一个,并定义了这两个rank在变化过程中的多个关键时间点。其中包括,如果在图中抹去v,顶点u首次变为被动匹配的时间点τ;如果在图中抹去u,顶点v首次变为被动匹配的时间点γ;以及,u处于主动情况下,v首次变为变动的时间点θ。接下来,通过反复利用二分图下的性质2,我们分析了yu,yv不同取值下的匹配情况,并获得如下不等式:
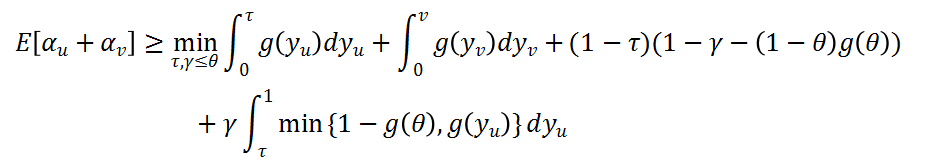
通过对收益分配函数g的优化,我们得到结论:当我们选择一个特别的分段收益函数g(y)时,我们可以证明了不等式右侧恒大于0.567。由此,我们证明了0.567的竞争比。
进一步,当考虑一般图情况时,我们面临了更大的挑战。由于性质2也不成立,仅考虑u,v两点的收益之和的方法大多都最终指向了0.5竞争比。这是由于在性质2被完全破坏的情况下,u,v的收益之和仅仅可以对边(u,v)的覆盖可能只能达到0.5。为解决这一情况,我们提出了一种受害者补偿策略:在u,v两点收益不足的情况下,寻求第三个点w进行补偿。值得注意的是,该补偿策略要兼顾平衡性。由于w会需要给出补偿,我们必须证明w是一个收益富足的顶点,可以在提供补偿的同时,兼顾对自身邻边的覆盖要求。为简单阐述受害者补偿策略的基本思路,我们考虑如下特殊情况:当v不匹配时,u与某顶点z匹配,并获得了1-g(θ)。而当v的rank提高进而被某顶点w匹配时,z被w原先的匹配顶点w主动选择,进而导致u不匹配,不能获得收益。(例子中w、w'、z、u、v形成了一个5个顶点的奇圈。)可以看到,在该特殊情况中,性质2被完全破坏,相比于v不匹配的情况,u的收益非但没有提高,反而完全消失。在该例子中,我们定义v为w的受害者,并要求w对v进行补偿。那么,为什么w可以提供补偿呢?这是因为我们发现w本身并不会对应地出现性质2被完全破坏的情况。考虑不匹配时,假如存在另一条需要覆盖的边(w,v'),且v’处于不匹配状态。那么v'在变为匹配后,w会变得不匹配吗?答案是不会的,因为w还存在v这一备选项,即使现有w匹配顶点被w'抢走,w依然可以选择v进行匹配。综上所述,我们定义v为的w受害者,并让w对受害者v进行补偿。于此同时,受害者会作为一个的备选项,在一定程度上确保不会进入不匹配状态。因此,对w来说,由于性质2被完全破坏的情况不会发生,他的收益能够突破0.5;对于v来说,由于在性质2被完全破坏的情况下,他将收到w的补偿,他的收益也足以突破0.5。通过对这两项额外收益进行权衡优化,我们证明了0.5211的竞争比。
参考文献
【STOC90】Karp R M, Vazirani U V, Vazirani V V. An optimal algorithm for on-line bipartite matching[C]//Proceedings of the twenty-second annual ACM symposium on Theory of computing. 1990: 352-358.
【SODA13】Devanur N R, Jain K, Kleinberg R D. Randomized primal-dual analysis of ranking for online bipartite matching[C]//Proceedings of the twenty-fourth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics, 2013: 101-107.
【JACM20】Huang Z, Kang N, Tang Z G, et al. Fully online matching[J]. Journal of the ACM (JACM), 2020, 67(3): 1-25.
【FOCS20】Huang Z, Tang Z G, Wu X, et al. Fully online matching ii: Beating ranking and water-filling[C]//2020 IEEE 61st Annual Symposium on Foundations of Computer Science (FOCS). IEEE, 2020: 1380-1391.
【Preprint 22】Tang Z G, Zhang Y. Improved Bounds for Fractional Online Matching Problems[J]. arXiv preprint arXiv:2202.02948.
(上海交通大学张宇昊供稿)